What is gomoku
Gomoku is a simple game, very similar to tic-tac-toe. It is played generally on a 15×15 squares board by two players. Each player has to put down it’s piece and the one that gets a ‘5 in a row’ (either vertically, horizontally or diagonally) wins!
It is a perfect information game and has simple rules, so it was a good playground for me to experiment basic AI algorithms, heuristics and code optimization.
I made an online demo of the game, check it out!

Minimax algorithm
The idea of the minimax algorithm is to describe the game as having a state and two players that alternate eachother in turns. It assigns to each state a score and, since gomoku can be considered a zero-sum game (meaning that the advantage of one player is equivalent to the disadvantage of the other player), one player wants to maximize the state’s score (called maximizer), while the other one wants to minimize it (called minimizer). In this case the GomokuAI will be the maximizer, while the human player will be the minimizer.
The minimax algorithm recursively explores all the future possible game states evaluating them. It represents this as a tree and as an output it suggest the current move corresponding to the higher score possible.
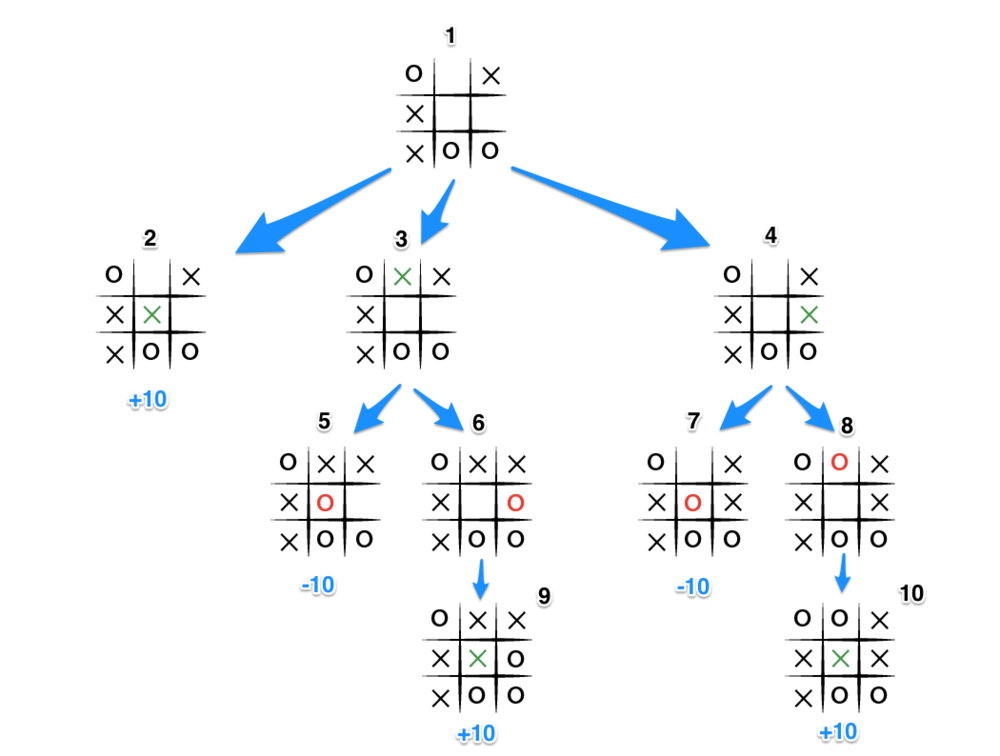
The algorithm is exponential, for the first move it has 225 choices and for each of them it has to consider every possible future move, thus only for the first two moves it has to compute 225*224=50400 states. It is clearly unfeasible to compute everytime every scenario development until the end of the game, so a maximum depth has to end the recursion. Furthermore not all possible moves are meaninful in order to maximize the score, thus in the following sections will discuss ways to prune some of the possible moves.
Score heuristic
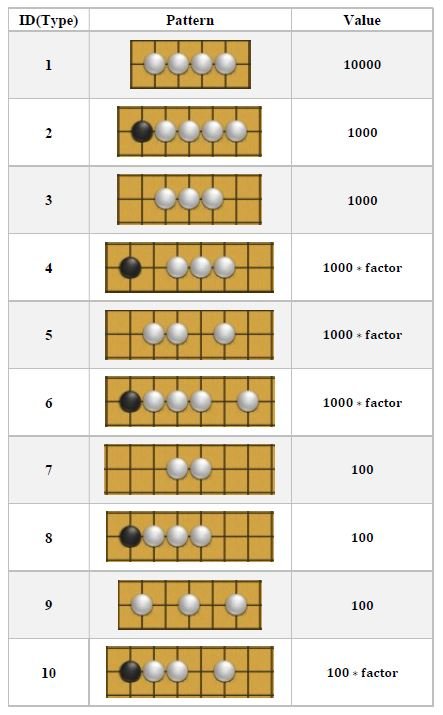
Since we cannot always visit the game states all the way to the game end we need a score heuristic to inform the AI bot how well is doing. This part of the algorithm building is the one that involves moe human knowledge since you have to know not only the basic rules of the game, but also be good at the game in order to evaluate it! Fortunately gomoku is pretty simple also from this perspective: we only have to look at the structures built. Of course a ‘5 in a row’ will always have the maximum score possible. Similarly a ‘live 4 in a row’ (meaning a for in a row that is not blocked on any side) will have near-maximum score, because whichever side the opponent will block I will still be able to win. On the other hand a ‘sided 4 in a row’ is not as useful, since if the opponent blocks the other way my structure will become useless so there is no point in trying to build such structure!
Going forward with this train of tought we can categorize all the possible (or meaningful) structures. Here is an example:
Alpha-beta pruning
Alpha–beta pruning is a search algorithm that decreases the number of nodes that are evaluated by the minimax algorithm in its search tree. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further.
The algorithm maintains two values, alpha and beta, which respectively represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of. Initially, alpha is negative infinity and beta is positive infinity, i.e. both players start with their worst possible score. Whenever the maximum score that the minimizing player (i.e. the “beta” player) is assured of becomes less than the minimum score that the maximizing player (i.e., the “alpha” player) is assured of (i.e. beta < alpha), the maximizing player need not consider further descendants of this node, as they will never be reached in the actual play.
Nearest squares search
Another way of reducing the search space is by involving (again) human knowledge. We know that if the game is evolving aroung the center of the board, putting a piece far away from the cluster that is being formed results kinda useless (a part from giving away the potential advantage that one can have build). So one way of reducing the search space is to allow the analysis of the moves that are near other pieces. This improves dramatically the speed of the search algorithm, especially in the early game as it goes from analysing ~250 possible moves per recursion to ~10 moves per recursion.

Threat sequences search
There are some scenarios where the move that one is supposed to make is obvious. These scenarios are so important that in other games, the rules of the game force you to take that action (in Chess, for example, if you are in check, you cannot do anything else but save the king, orelse you will lose). In Gomoku there exist such scenarios too: let’s say that it’s my turn and I have a ‘live 3 in a row’ (meaning that my 3 in a row is not blocked from any side), it would stupid not creating a ‘live 4 in a row’ (which leads to a win as explained before). Having this knowledge we can tell the algorithm that in such scenarios only the ‘obvious moves’ are to be analysed. This reduces again the search space, thus the computational time!

Comments are closed